پیشرفت های پنهان سازی برای امواج خمشی در صفحات الاستیک

کار قبلی در مورد پوشش برای امواج خمشی در صفحات الاستیک محدودیت‌ها و تقریباً نامرئی بودن را نشان می‌داد. اکنون، یک گروه تحقیقاتی در اروپا چارچوب نظری جدیدی را برای غلبه بر محدودیت‌ها و دستیابی به پوشش دقیق برای امواج خمشی در صفحات Kirchhoff-Love کشف کرده‌اند . برای تجسم و آزمایش کیفیت شنل، آنها شبیه سازی COMSOL Multiphysics را اجرا کردند.

توضیح مختصری از تبدیل های پنهان سازی

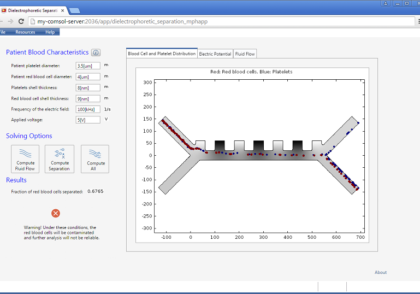
این را تصور کنید: امواج خمشی وجود دارد که از منبعی در یک صفحه الاستیک نازک ساطع می شوند. اگر جسمی را در بشقاب قرار دهید، امواج را به هم می زند و می توانید آن را ببینید. اگر به جای آن روپوشی در اطراف جسم قرار داده شود، امواج مختل نمی شوند و در نتیجه جسم نامرئی می شود.

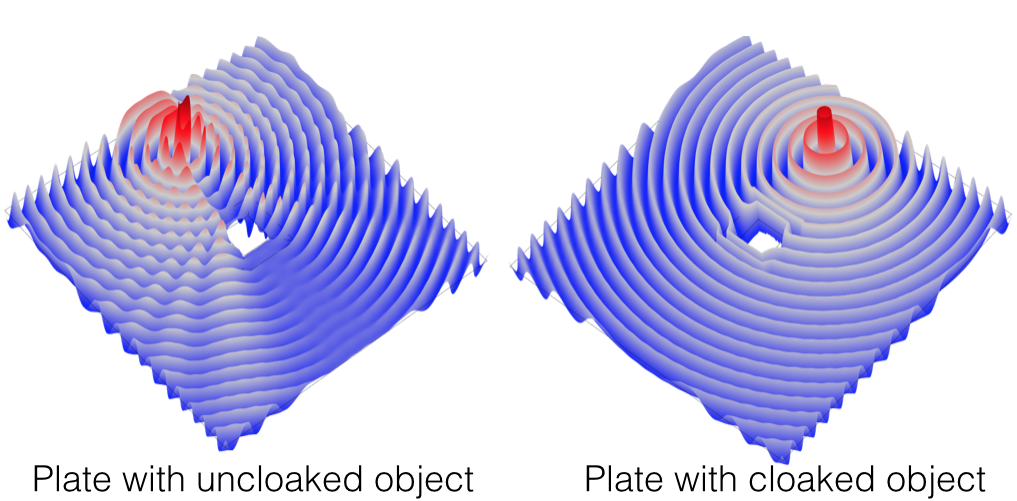
شیء بدون و با پوشش.
مدل‌هایی که یک شی را بدون پوشش و با پوشش نشان می‌دهند. ارائه شده توسط Daniel J. Colquitt.

در حالی که درک این مفهوم به اندازه کافی آسان است، درک آن چندان آسان نیست. برای پوشاندن یک شی، شما باید متاماده مناسبی بسازید (فراماده در طبیعت وجود ندارند، آنها مواد مصنوعی هستند که برای داشتن خواص خاص مهندسی شده اند).

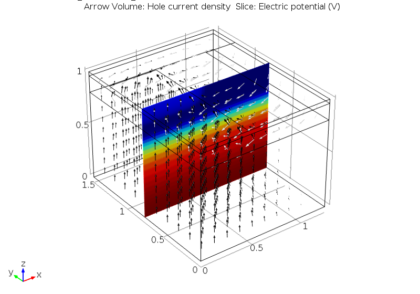
فرامواد را می توان به گونه ای طراحی کرد که خواص مواد آنها تغییرات فضایی ایجاد شده توسط دگرگونی های مختصات را تقلید کند، در نتیجه نور، صدا یا امواج دیگر را به شیوه ای خاص هدایت می کند. پیکربندی اولیه میدان های الکترومغناطیسی یا آکوستیک روی یک مش دکارتی ترسیم می شود که سپس برای تبدیل مختصات پیچ خورده است.

تصویری که یک مش دکارتی پیچ خورده را نشان می دهد.
تصویر مش دکارتی تابیده نشده.

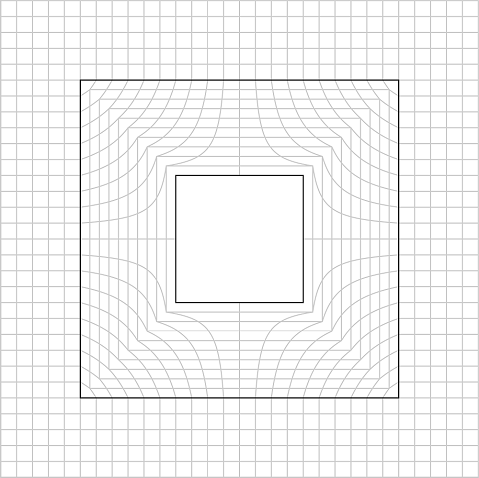
مش پوشش پیچ خورده.
مش پیچ خورده. ارائه شده توسط Daniel J. Colquitt.

پوشاندن نور و صدا

وقتی صحبت از پوشش الکترومغناطیسی و آکوستیک به میان می آید، به ترتیب از معادلات ماکسول و معادله هلمهولتز استفاده می کنید. هر دوی این معادلات در هنگام تبدیل مختصات ثابت هستند ، به این معنی که در فرآیند تغییر نمی‌کنند.

پنهان کردن امواج مکانیکی

با این حال، اگر می‌خواهید به صورت ریاضی پوشش را برای امواج مکانیکی، مانند امواج خمشی در صفحات الاستیک مدل کنید ، به یک معادله دیفرانسیل جزئی مرتبه چهارم (PDE) نیاز دارید. شکل کلی PDE ثابت نیست . در طول تبدیل مختصات تغییر می کند.

کارهای قبلی با استفاده از الاستودینامیک تبدیل برای دستیابی به cloaking با رشته هایی متصل بود. به دنبال برخی چارچوب های قبلی، محاسبات چگالی کششی و تنش های نامتقارن را به دست آوردند. تحقیقات دیگر چارچوبی را ایجاد کردند که در آن PDE می‌توانست روی صفحات نازک اعمال شود، اما فقط برای تئوری‌های غیرخطی.

کاربر COMSOL Multiphysics، Daniel J. Colquitt و همکارانش بالاخره در حال شکستن محدودیت‌های این نوع طراحی پنهان‌سازی هستند.

غلبه بر محدودیت ها: پوشش برای امواج خمشی در صفحات الاستیک

در مقاله “الاستودینامیک تبدیل و پوشش برای امواج خمشی”، DJ Colquitt، M. Brun، M. Gei، AB Movchan، NV Movchan و IS Jones یک چارچوب جدید برای الاستودینامیک تبدیل برای صفحات نازک و یک الگوریتم برای طراحی شنل پهن باند ارائه کردند. . صفحات الاستیک نازک با صفحات Kirchhoff-Love نشان داده می شوند – یک مدل ریاضی دو بعدی که معمولاً برای مشخص کردن صفحات نازک استفاده می شود.

Colquitt در یک مکالمه ایمیلی برای من توضیح داد: “معادلاتی که بر جابجایی خمشی صفحات الاستیک نازک حاکم هستند با معادلات مربوط به نور و آکوستیک (به عنوان مثال، معادله هلمهولتز) بسیار متفاوت است. او افزود: «در واقع، معادله حرکت برای امواج خمشی شامل عملگر بی هارمونیک است که یک عملگر دیفرانسیل جزئی مرتبه چهارم است. این برای سیستم‌های فیزیکی که در آن معادلات حرکت معمولاً مرتبه اول یا دوم در فضا هستند (مثلاً الکترومغناطیس، آکوستیک، الاستیسیته) نسبتاً غیرمعمول است.

بنابراین چگونه محققان بر مسئله واریانس معادله در طول تبدیل مختصات غلبه کردند؟ آنها با معرفی یک مدل صفحه تعمیم یافته، به معادله تبدیل شده یک تفسیر فیزیکی دادند. در این چارچوب جدید، شنل نامرئی با اعمال ترکیب خاصی از نیروهای پیش تنیدگی و بدن بر روی یک صفحه فرا ماده ایجاد می شود. بر خلاف سایر چارچوب ها، فریم ورک جدید کاملاً خطی است. آنها همچنین نشان می دهند که الگوریتم جدید آنها با موفقیت تنش های متقارن و چگالی اسکالر را تضمین می کند.

قدرت وارد کردن معادلات خودتان

برای تجسم نتایج cloaking و آزمایش کیفیت شنل، Colquitt و همکاران. شبیه سازی ها را با استفاده از نرم افزار COMSOL Multiphysics ایجاد کرد. ظاهراً، هنگام تصمیم‌گیری از اینکه کدام نرم‌افزار برای آزمایش شنل آن‌ها استفاده شود، انعطاف‌پذیری یک عامل کلیدی بود.

شنل نامرئی مستلزم اجرای یک صفحه ناهمگن و ناهمسانگرد است که در معرض نیروهای پیش تنش و بدن ناهمگن و ناهمسانگرد قرار دارد. همانطور که می توان تصور کرد، معادلات حاکم برای این سیستم غیر استاندارد هستند. “COMSOL به ما اجازه داد تا به طور مستقیم شکل دقیق معادلات حاکم تغییر یافته را پیاده سازی کنیم. این برای یک ریاضیدان بسیار جذاب است – توانایی کنترل مستقیم سیستم معادلات در حال حل.

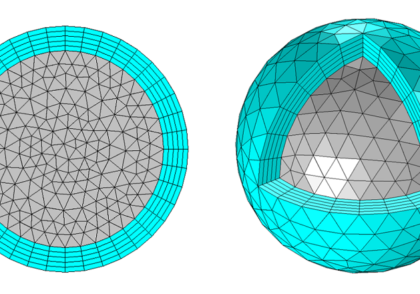
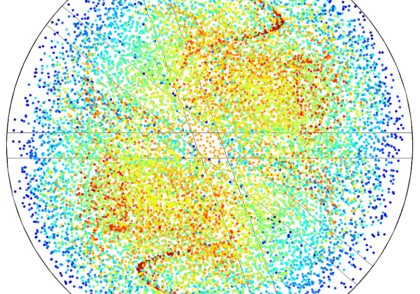
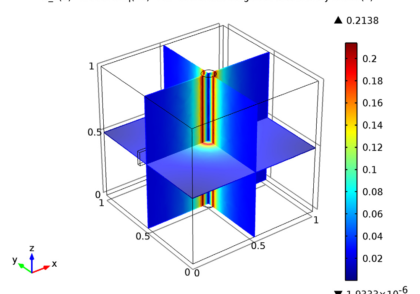
در زیر چند تصویر و انیمیشنی که نتایج آنها را نشان می دهد، آورده شده است.

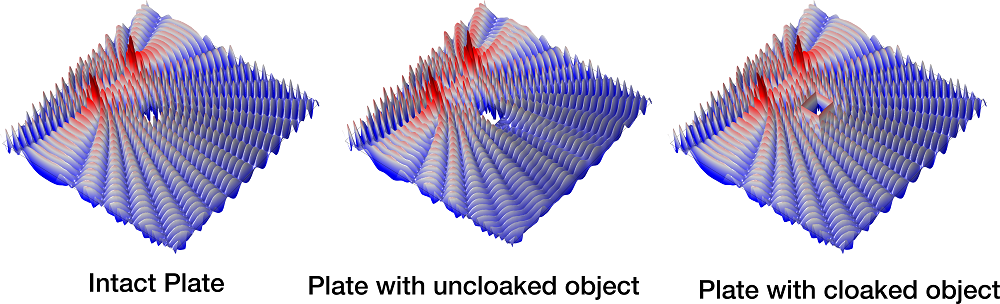
نتایج پنهان سازی ارائه شده توسط Daniel J. Colquitt.

انیمیشن جسم مربعی پوشیده شده در حال حرکت در امواج خمشی در صفحه نازک. با حسن نیت از Daniel J. Colquitt.

کاربردهای تحقیقاتی

بنابراین، محققان با موفقیت یک چارچوب نظری جدید را توسعه داده‌اند که به آزمایش‌گران اجازه می‌دهد تا پوشش‌های مکانیکی نامرئی را طراحی و بسازند که می‌تواند اشیاء را از ارتعاشات مکانیکی پنهان یا محافظت کند.

در مورد استفاده از چارچوب، Colquitt گفت: “کاربردهای بالقوه زیادی مانند پنهان کردن یا جداسازی قطعات حساس تجهیزات از ارتعاشات مکانیکی با مسیریابی امواج خمشی در اطراف تجهیزات وجود دارد.”

به طور خلاصه، این تحقیق بسیار جذاب است و من به شدت توصیه می کنم مقاله (لینک زیر) را بخوانید تا دامنه کامل کار آنها را دریافت کنید.